Programming for Speed

In the cells below I give some rules of thumb that enhance the speed of
Mathematica programs.

Use look up tables

When you have values for (f) defined for specific values such as

f[1]=y1;

f[2]=y2;

f[3]=y3;

  ...

Mathematica can evaluate something like f[2] with great speed. The speed of
evaluation is very fast for definitions that are free of patterns such as x_
or {x_,y_}. I refer to storage of function values for specific arguments as a
look up table.



For example you could define a new version of Prime that evaluates over a
certain range of large integers much faster than the built-in Prime function.
The next cell defines MyPrime which uses Prime for n<5000000000, and has
explicit values stored for 5000000000<n<5000000010.  I felt it would be
appropriate to first try the rules for 5000000000<n<5000000010 so I rearrange
the list of DownValues. The output below shows the resulting list of
definitions.

Now in the next cell I do the same thing with explicit values stored for
5000000000<n<5000010000, but display of the list of rules is suppressed
because it's very long. You should be patient when the next cell is evaluated
because it takes several minutes.

Once the definitions for MyPrime are stored a list of primes can be made with
the next cell almost instantly.

An  implementation with more sensible use of memory would only store explicit
definitions of MyPrime for say 5000000500, 50000001000, 5000001500,
5000002000, ... and would evaluate Nest[NextPrime,MyPrime[50000001000],43] to
determine MyPrime[50000001043]. I didn't do that here because my purpose here
is to demonstrate how fast the lookup table is.



Often times look-up tables are created on the fly using definitions of the
form:

f[x_]:=f[x]=expr

This can result in efficient programs if (f) needs to be evaluated many times
for the same argument.

Use functional programming

The tools of functional programming include:

   Map  MapAt  Thread  Apply  MapThread  MapAll  MapIndexed  Fold  FixedPoint
Nest  NestWhile

   FoldList  FixedPointList  NestList  NestWhileList  Scan  Inner  Outer  
Distribute.

Each of these are often an important part of very efficient programs.



Other functional programming tools available are:

    ComposeList, Composition  Operate  Through.

These other functional programming features are also efficient, but seldom
needed in practice.



No examples of the functions listed above are provided here, but many of them
have a devoted section in this notebook

Use pure functions

In the next cell three similar functions are defined . The function f1 is
defined with a named pattern while pure functions are used to define f2 and
f3. We see the implementation defined with pure functions run much faster
than the definition defined with a named pattern.  Also the short hand form
(6 #+13)&  runs a bit faster than Function[x, 6 x+13].

Use "linked lists" instead of adding to a list

The most straight forward way of adding to a list uses PrependTo or AppendTo
as in the next cell. There are a number of other ways you could effectively
do the same thing but they are all very slow for making long lists. As an
example consider the program in the next cell which makes a list by
prepending values.

The faster way to build the list in the previous cell is to make a linked
list which looks like  

{... ,y4,{y3,{y2,{y1}}}} instead of {...  ,y4,y3,y2,y1} as returned by the
program in the previous cell. Flatten can then be used to convert the linked
list into a flattened list.

However a temporary head is needed if you want to quickly build up a list
such as

{... ,{x4,y4},{x3,y3},{x2,y2},{x1,y1}}. In that case an expression with the
form

h[{x4,y4},h[{x3,y3},h[{x2,y2},h[x1,y2]]]] can be built-up. Then you can get
the desired result by flattening the nested list and changing the head (h) to
List. This is done in the next two cells.

Avoid use of AppendTo and PrependTo

Use of PrependTo and AppendTo is not a problem if they only evaluate a few
times.  But your program will be very slow if they evaluate many times.  This
point was made in the previous rule of thumb.

Don't compute the same thing over and over

Often times one needs to have an understanding of the evaluation process to know when things are computed over and over.  An example of this point  is given in the section on Set versus SetDelayed which is copied below.

Alan Hayes provided the code in the next cell as an example where (   func[x_]=  ) should be used instead of ( func[x]:=  ).
If we did use (  func[x_]:=  ) in this example the least squares fit would be computed  again  for every value of (x) when we evaluate something like
Plot[curve[t],{t,0, π/3}].

Use the simplest form possible

Some Mathematica functions are special cases of other functions. An example
of this is Range which is a special case of Table. Hence Range will make a
list in the next cell faster than Table would.

Lots of Mathematica functions have multiple forms available. In many cases
simpler forms are available which are special cases of more general forms.
Hence Table runs faster in the next cell when an iterator isn't used.

Minimize the number of expressions the kernel must evaluate

Ensuring that a program needs to evaluate the fewest number of expressions is
an important part of minimizing the time a program needs to evaluate. For
example the Dot product of two vectors evaluates much faster when the built
in Dot function is used in the next cell.  Here the slow version evaluates
Part 100 times, Times 50 times and one call to Sum.  The fast version makes
only one call to Dot.  Clearly Dot must multiply respective parts of each
list, but it does so much more effeciently than we can with the slow version.

Another example (which only works in Version 4 or later) is given in the next
cell where the slow method of making a list needs to evaluate Part 12 times,
but the fast method does the same thing in one application of Take.

Still another example (which only works in Version 4) is given in the next
cell where the slow method maps First onto each element of data, but the fast
method does the same thing with one application of Part. When the slow method
is used First must be evaluated over and over.

In the next cell we can use Table and Take to split up a list into sublists.  
The built-in function Partition is designed just for this purpose and does
the job much faster.

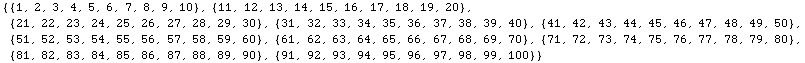
Other special purpose functions are ListConvolve, ListCorrelate, Split,  Ordering, and Tr to name a few.  Any direct use of these functions is  probably faster than doing the same thing with some Mathematica code you might write.

Another example of this principle is changing the value at multiple parts  of an expression by using the Part feature only once. This is demonstrated in  the section on Part.

Use approximate machine numbers whenever appropriate

If your application can tolerate the round off error inherent in machine
precision arithmetic you can greatly improve the speed of your program by
ensuring all numeric calculation is done on approximate machine numbers. Of
course certain calculations over integers (e.g. multiplication and addition)
are quickly computed over machine integers and computing with approximate
numbers would not be any faster in that case.

Use Packed Arrays

Rob Knapp provides a tutorial on Packed Arrays at  http://library.wolfram.com/database/TechNotes/391/. and I give simplified examples of the trick he uses to speed up an  implementation of LUDecomposition above in my discussion of Part.

As Rob explains you often need to use certain programming methods to  get the improved speed possible with the with Packed Arrays.
To start with  you only get the benefit of packed arrays when your data structure can fit in  a packed array.  For more on this subject see chapter 6 (Performance) at:
http://documents.wolfram.com/v5/Built-inFunctions/ AdvancedDocumentation/LinearAlgebra/.

Use Compile effectively

The speed of programs can often be enhanced if they are written using  Compile, but you need to take certain steps to ensure the program evaluates  with compiled evaluation. This is discussed in the section on Compile.  As I mention in that discussion only certain types of work can be done  with compiled evaluation.

Don't use ReplacePart, MapAt or Insert when the last argument is a

long List (>40).

ReplacePart, MapAt and Insert are very slow in this case. For mor  explanation see the discussion of Slow Kernel Functions.

Be careful about modifying large data structures in place over and over

This discussion on modifying large data structures comes from  "Power  Programming with Mathematica The Kernel"  by David B. Wagner.

This isn't  so much a rule of thumb, but a trick that is useful in special cases.  Consider computing a moving average of a list of numbers.  With the first  approach below we use (s) as our input and output.  As explained where I  discuss the Mathematica evaluation process each element of (s) is evaluated again each time s[[i]] is accessed  because (s) was modified since it was last used.  All the exccess evaluation  is very inefficient and the time needed with this approach is proportional to  the square of the length of the list.

By simply hanging the head of the list to HoldComplete the exccess evaluation
is prevented, and the time needed is directly proportional to the length of
the list.  At the end we change the head back to List.

It's even better to avoid a procedual approach all together as I do in the
next cell.  The performance gain here is largely due to reducing the number
of expressions that need to evaluate (one of my other rules of thumb).



However, in some cases the HoldComplete trick above provides the best
solution.

Beware of inefficient patterns

Most of this discussion on inefficient patterns is from "Power  Programming with Mathematica The Kernel" by David B.Wagner.

An  implementation of run length encoding is given below.  This implementation  written by Frank Zizza is clearly elegant and it even won an award in a  programming contest at a 1990 Mathematica conference.

In the next cell we see an example using runEncode.

Next we see that runEncode takes a long time to encode a list of 2000
integers.  In fact the time it takes this implementation to finish is
proportional to the square of the length of the list, and this is not good at
all.

The reason this implementation performs poorly is because of the way the  kernel performs pattern matching. In the next cell we see pattern matching in  action by causing the replacement to print each attempt at matching the  pattern.

There are two important points about this result.  First, the  kernel attempts to match sequence patterns (e.g.  __, ___, Repeated, RepeatedNull) from left to right.  Second, once the kernel finds a succeful match for  the pattern, it starts the comparing patterns for the next iteration at the  left end of the input, which for this particular algorithm is a guarenteed  waste of time.

Below I give a run length encoding implementation that performs much better.  
Unfortunately the implementation below is more difficult to understand.  You
will find the time this implementation takes is directly proportional to the
length of the input list.

Below we see that the second implementation performs much better.

Check These Sources Too

http://library.wolfram.com/infocenter/Conferences/388/
http://library.wolfram.com/infocenter/Conferences/320/
http://library.wolfram.com/infocenter/Conferences/422/
http://library.wolfram.com/infocenter/Conferences/321/
http://library.wolfram.com/infocenter/Conferences/367/

Also see Alan Hayes in-depth articles on efficient Mathematica programming in The Mathematica Journal which are posted at
http://www.mathematica-journal.com/issue/v2i2/  and  http://www.mathematica-journal.com/issue/v5i1/.

Chapter 10 of

Power Programming with Mathematica The Kernel  

by David B. Wagner  (ISBN 0-07-912237-X)  

gives more advice on improving the speed of Mathematica programs.  

Unfortunately this great book is out of print, but you may be able to get a
copy from an online auction such as e-bay or from the amazon.com out of print
book service.

Created by Mathematica  (May 17, 2004)